Technology in context

Rough few weeks – sorry for no post. But here’s something that people might find useful.

This semester at Penn, I’m taking a compilers course (CIS341). It’s been a blast – we’re developing a compiler for a language called OAT (as in Quaker Oats) that’s ‘objects, arithmetic, and types’. Due Monday is the object compiler, and the language is done in its entirety.The last two projects concern optimizations (register allocation, constant propagation, etc).

Writing compilers, for anybody who hasn’t done it before, involves a tremendous amount of work. Because compilers have always seemed like magic to me, I’m going to attempt to demystify them.

This will be a several-part tutorial written as I have time, so check back often.

I will assume you know something about programming, and are willing to learn a crash-course in formal languages, but I’ll try to keep it simple. By the end, we’ll have a reasonably interesting compiler for basically the language I’m writing now. The only thing is, we’ll do it in C instead of OCaml, which is what I’m using now. This is partly because most compilers are written in C, or their own languages, and partly because I don’t want to enable cheating.

Alright! Here we go. To start, we need to discuss formal languages – what they are, what they can do, and how to work with them. Next time, we’ll get into actual code.The first two steps are common among all compilers, and thus are very automated.

Time for some theory. Computer languages are formal languages, specifically (in most cases) a context-free grammar. For anybody who hasn’t taken an automata class (lucky  you), this is something like “the language containing all strings of matched parentheses”. Languages, in this case, are sets of strings. So our language of matched parentheses would accept “”, “()”, “(()()(()()))”, but not “(()”.

By way of demonstration, let’s look at the grammar (rules for how to build a string) of our parenthesis-language:

E -> ε | EE | (E)

‘E’ is a ‘nonterminal’. You can think about it like a variable. ε is a ‘terminal’ – you can think of it as a character, though ε actually means ‘nothing’. Now pretend this rule is a recursive function that accepts E, and returns either ε (the base case) or (E)- that is, E evaluated recursively, surrounded by parenthesis, or EE evaluated similarly.. It’s a little mind-bending, but the basic idea is that these rules make it impossible to generate strings not in the language. We’ll see why this last rule is is necessary.

Don’t believe me? Let me demonstrate how to generate the three strings I gave above:

• “”: E->ε = “”
• “()”: E->(E)->(ε) = “()”
• “(()()(()()))”: E->(E) -> (EE) -> (E(E)) -> (EE(E)) -> (EE(EE)) -> ((E)E(EE)) -> ((E)(E)(EE)) -> ((E)(E)((E)E)) -> ((E)(E)((E)(E))) -> (()()(()()))

As you can see, if I follow the rules of the grammar I can’t help but come up with well-formed strings. As you’ve probably figured out, the last rule is necessary because otherwise you could only come up with one set of nested parenthesis like “((()))”, not multiple like above

This language is context-free because it doesn’t “count”. It’s hard to explain in layman’s terms, but because “context-free” in this context (heh) means that it doesn’t “remember” anything, the language of 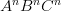(the same number of A’s, B’s, and C’s) is not context-free. I could do 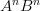(exercise: do this), but because I have no way to add C’s at the same time as A’s or B’s, I can’t restrict it to a count of n. It makes more sense if you read about pushdown automata, but you might find that you need a much larger background in automata theory to understand it.

But programming languages, as a rule, are context-free, mostly because grammars make it easy for programs to understand them. There is a well-understood technique called “parsing” for taking a context-free grammar and a string, and coming up with a “parse tree”. This is like going backwards – instead of starting with the grammar and working through it to come up with a string, we start with the grammar and a string and work backwards to figure out how to use the grammar to come up with it. Back to our parentheses, the root of this tree is the E, and it branches out with each rule.

Programming languages have much more complicated grammars than the ones we’ve looked at. For example, here’s a bit of the C language grammar (it’s several pages long – you can find it online, or in the back of K&R) expressed in Baukus-Normal Form (BNF):

iteration-statement:
    while ( expression ) statement
    do statement while ( expression) ;
    for ( expression_opt : expression_opt : expression_opt ) statement

jump-statement:
    goto identifier ;
    continue ;
    break ;
    return expression_opt ;

This ought to be pretty straightforward, particularly if you’ve ever used C. In case it’s not clear, things like ‘iteration-statement’, ‘statement’, ‘expression’, and so forth are nonterminals, just like E was. But as you can see, it’s the same idea as we were doing above – if you follow the rules, you can’t help but come up with a valid C program, at least from a grammatical standpoint. And as I was also saying, you can use a parser to come up with the tree that represents this code.

Now you know the first step of coming up with a language – you need to define its grammar so that you know what a valid program looks like. It sounds like a daunting task, and it is – you’ll probably want to read more about context-free grammars to get a sense for some of the nuances, particular ambiguity. There’s about half of a college course in the above tutorial, so it’s necessarily incomplete and simplified – but it should be pretty straightforward. Feel free to let me know below if you’d like clarification.

Next is part 2 – lexing.